Deterministic creation of up to five-qubit W states demonstrated on a real quantum computer

The seminal article by Dür, Vidal and Cirac [1] not only emphasizes the interest of entangling three qubits in a W state in quantum computing and cryptography, but also introduces the notion of generalization of a W state to a multi-qubits system. Numerous experimental achievements of GHZ multi-qubit entanglement are reported, for example the demonstration of a five-photon entanglement by Zhi Zhao et al [2]. However, to our knowledge, there is currently no reported demonstration of multi-entanglement of four or five qubits in W state, although the theoretical basis of the appropriate experimental schemes are proposed repeatedly in the literature. Among these theoretical contributions, a recent article by Firat Diker [3] proposes an algorithm in the form of nested boxes allowing the deterministic construction of W states of any size. The experimental setup proposed by the author is essentially an optical assembly including half-wave plates.
After having demonstrated somewhere else on this blog the production of 5-qubits GHZ states on the ibmqx4 for testing Mermin inequalities, it was tempting to see if the Diker algorithm could produce a similar type of multi-entanglement for W states on the same system. To do this, the theoretical presentation had to be adapted to meet the requirements of programming specific to the project "IBM Q experience". The model had also to be adapted to the connectivity map of the ibmqx4. This adaptation finally has the advantage of avoiding confusion between the formulation of Diker and that of the IBM Q experience, for example between Diker box U (which becomes box M) and universal gate U3.
Theoretical model
The creation of a circuit for obtaining a state W of n qubits requires a series of boxes Mk , k=2...n, nested in the manner of a set of Matryoshka dolls. The circuit for n = 5 for an ideal quantum computer where all the qubits are interconnected in a bidirectionnal manner is shown in FIG1.
The nesting of the Mk boxes is described by the following set of equations:
(eq.1)
The schema of the Tk operators is represented in FIG2. These operators include y-rotation gates and 2-qubit cZ gates.
The y-rotations are obtained on the composer of the ibmqx4 by using the universal gate U3 with parameters 𝜃= 𝜃k , 𝜑 = 0, 𝜆 = 0, in accordance with the following equality:
Ry(𝜃) = U3 (𝜃,0,0) (eq.2)
If qubitc is the control and qubitt is the target, a cZ gate consists of a sequence of a first H gate on qubitt, a cNOTct gate and a second H gate on qubitt. The angle 𝜃k for a Tk operator is :
𝜃k = arc cos (1/√k) (eq.3)
The Tk operator corresponds to the Diker two-qubit F gate and works thus as follows:
 |
| (eq.4) |
The Bk operators are sequences of cNOT gates where the target is always the kth qubit, of the following form (the order does not matter) :
| (eq.5) |
In order to create a n qubits W stage |Wn⟩, we first apply an X Pauli gate to the nth qubit to create the initial state:
| (eq.6) |
Using the equation set 1 and the equations 4 to 6, it is easy to show that, for any n ≥ 2:
| (eq.7) |
It should be noted that according to this formulation |W2⟩ is actually the well known Bell state
|Ψ+⟩.
|Ψ+⟩.
Experimental setup
In order to program the real quantum computer, it is necessary to substitute the connections that cannot be made by reverse gates and to perform qubit swapping at appropriate times. The gates used for this purpose are shown in FIG3. Details concerning the reverse cNOT and the swap gate can be found here: https://quantumexperience.ng.bluemix.net/qx/tutorial?sectionId=full-user-guide&page=004-Quantum_Algorithms~2F061-Basic_Circuit_Identities_and_Larger_Circuits
 |
| FIG3: Some useful gates used in the circuits |
Armed with these instruments, it is then possible to adapt the ideal schema to the connectivity map of the ibmqx4 in order to realize real-world experiments (FIG4).
 |
| FIG4: Adaptation of the nested box model to the ibmqx4 quantum computer in order to create a 5-qubit W state. The color code for the set of Matryoshka dolls is the same as in FIG1: M2 M3 M4 M5. |
Programming:
The programming for each of the circuits giving rise to the states |W2⟩ to |W5⟩ was done using the QISKit SDK python platform and the Composer module of the IBM Q experience.
Each program written in python was tested first on the local simulator (8192 runs), then on the ibmqx4 (1 run). From the OPENQASM listing obtained for the ibmqx4 pilot experiment, a modified listing adapted to the Composer was obtained by going through an editing phase in Microsoft Words. This version was then pasted into the QASM editor of the Composer. The partitions (FIG5) corresponding to this modified program were inspected to ensure the presence of adequate barriers between the H gates following each other.






 |
| FIG5. Two-qubit to five-qubit W-state circuits |
 |
| FIG7. Histograms obtained using QISKit SDK python program with the ibmqx4 as backend |
For the circuits |W2⟩ to |W4⟩, the predominance in terms of frequency of the results compatible with a W state is obvious.
For the |W5⟩ circuit, the highest frequency observed is for the non-compatible result c5=00000 but the three following results in terms of frequency are : 10000, 00100 and 01000, all compatible with a W state. The two remaining compatible results 00001 and 00010 are more rarely observed.
|
FIG8 shows the histograms obtained for the circuits |W2⟩ to |W5⟩ using the Composer on the ibmqx4.

The predominance of the results compatible with a W state is again obvious for the circuits |W2⟩ and |W3⟩. For |W4⟩ however, the non-compatible c4=0000 result seizes the fourth position and the compatible result 0010 passes in fifth position in the order of the observed frequencies.
For the |W5 ⟩ circuit, the highest frequency observed is for the compatible result c5=00100. The non-compatible result 00000 is in second position, followed by the compatible results 10000 and 01000. Although absent from the leading pack, the compatible results 00001 and 00010 rank among the top nine in terms of frequency.
An estimation of the classical fidelity was obtained by calculating the Bhattacharyya coefficients for the measurement performed by running circuits |W2⟩ to |W5⟩ (FIG9).
 |
| FIG9 Estimation of the classical fidelity |
Discussion:
As might be expected, the frequency of the results compatible with a state |Wn⟩ decreases as a function of n. One obvious cause is the increase in the number of gates. For an ideal quantum computer, where all the qubits are connected together bidirectionally, the number of cNOT gates, Ry gates and H gates increases linearly for the operators Tk, while for the operators Bk, the number of cNOT gates which are their only constituents increases in a quadratic way, following the triangular numbers sequence. It follows that the total of the cNOT gates of a circuit creating |Wn ⟩ will be: ½(n² + n) - 1 in such an ideal machine.
For a real computer, it is necessary to add the number of cNOT and H gates constituting the reverse cNOT gates and the necessary swappings. For the ibmqx4, for example, these additional gates are visualized in the diagram of FIG4.
Another cause of error may be the interval between successive values of 𝜃k which decreases significantly as n increases, as can be calculated according to eq.3. The equivalent for an optical setup of this possible experimental imperfection was already pointed out by Diker [3], who mentioned that a small change of the angle of a single half-wave plate can lead to failure to creation process.
It must also be taken into account that the experiments reported here were performed on a superconducting quantum computing system using transmon qubits in ground and excited states, while those proposed in ref.[3] are planned for an optical system using a source of photons horizontally and vertically polarized. This makes any comparison of expected or observed error rates between the two approaches highly questionable.
It must also be taken into account that the experiments reported here were performed on a superconducting quantum computing system using transmon qubits in ground and excited states, while those proposed in ref.[3] are planned for an optical system using a source of photons horizontally and vertically polarized. This makes any comparison of expected or observed error rates between the two approaches highly questionable.
Conclusion:
The deterministic creation of W states up to five qubits has been demonstrated here experimentally on a real superconducting quantum computing system.
The Matrioshka doll-like nesting box algorithm proposed by Firat Diker appears to be both relatively simple and powerful.
However the algorithmic power mounts against a limit for the number of involved qubits. This is probably due mainly to the quadratic growth of the number of gates necessary to constitute multi-entanglement circuits concerning more and more qubits, but also to the need for y-rotations less and less distinguishable from each other.
However the algorithmic power mounts against a limit for the number of involved qubits. This is probably due mainly to the quadratic growth of the number of gates necessary to constitute multi-entanglement circuits concerning more and more qubits, but also to the need for y-rotations less and less distinguishable from each other.
There is good chance that such an algorithm will find its place during the development of quantum computers, for the transmission and preservation of data in particular, but also in quantum cryptography.
Some features of this working algorithm, e.g. the fact that it is nested and also that the amount of components grows according to the triangular numbers sequence opens the way to an intriguing assumption: some natural structures could be a spontaneous source of W states, in particular among heterostructures made of crystalline material or even highly complex structures encountered in living organisms.
[2] Z. Zhao, Y.-A. Chen, A.-N. Zhang, T. Yang, H. Briegel, and J.-W. Pan, Nature 430, 54 (2004), ISSN 0028-0836, quant-ph/0402096, URL http://dx.doi.org/10.1038/nature02643.
[3] F. Diker, Deterministic construction of arbitrary w states with quadratically increasing number of two-qubit gates (2016), 1606.09290, URL http://arxiv.org/abs/1606.09290.
I acknowledge use of the IBM Quantum Experience for the works presented here. The views expressed are those of the author and do not reflect the official policy or position of IBM or the IBM Quantum Experience team.
References:
[1] W. Dür, G. Vidal, and J. I. Cirac, Physical Review A 62, 062314+ (2000), ISSN 1050-2947, quant-ph/0005115, URL http://dx.doi.org/10.1103/physreva.62.062314.[2] Z. Zhao, Y.-A. Chen, A.-N. Zhang, T. Yang, H. Briegel, and J.-W. Pan, Nature 430, 54 (2004), ISSN 0028-0836, quant-ph/0402096, URL http://dx.doi.org/10.1038/nature02643.
[3] F. Diker, Deterministic construction of arbitrary w states with quadratically increasing number of two-qubit gates (2016), 1606.09290, URL http://arxiv.org/abs/1606.09290.
I acknowledge use of the IBM Quantum Experience for the works presented here. The views expressed are those of the author and do not reflect the official policy or position of IBM or the IBM Quantum Experience team.








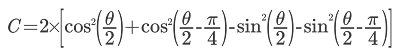
Comments
Post a Comment