GHZ States and Mermin Inequalities on a Five-Qubit Quantum Computer
The architecture of the new quantum computer ibmqx4 makes it possible to create a simplified circuit to produce the GHZ state involving up to five qubits. On the other hand, the new QISKit tutorial offers programming examples different from those offered in the beginner and full user guides made available by IBM since the beginning of the project. In particular, the GHZ states studied in the tutorial are of the type: ( |0...0> + |1...1> ) / sqrt(2) where a plus sign instead of a minus sign makes the difference with the guides versions.
This was an opportunity to re-examine the utility of a five-qubit quantum computer in the study of GHZ states and associated Mermin inequalities.
Three-qubit GHZ-state and Mermin inequality.
In this section, the programmation and results using a set of three qubits is briefly reported.
For those who have a Python environment and have installed QISKit, the program changes are basic. In addition to replacing ibmqx2 with ibmqx4 in the backend definition lines, the following circuit changes:
In [19], lines 7-9 and [21, lines 5-7:
For those who prefer to use the composer, a series of four experiments is also proposed (Figure 1). The results can then be retrieved as *.csv files to perform the calculations.
The set of observables remains the same as that used in the original program of the QISKit Tutorial:
The results obtained using QISKit are presented in Table 1 and Figure 2.
The Mermin polynomial for 3 qubits is obtained by adding the absolute values of the figures present in the last row of Table 1. We obtain 2.99, that is a value slightly higher than the value of 2.65 calculated according to the results reported in the full user guide (here) or the value of 2.85 reported by Alsina and Latorre (there). The current result is well beyond the upper bound for local realism, which is 2, while the theoretical upper bound for quantum theory is 4.
The inspection of Figure 2 reveals the contrast between the distribution observed for the experiment XXX and those observed for the experiments XYY, YXY and YYX. The latter are all alike.
In [19], lines 7-9 and [21, lines 5-7:
ghz.h(q3[0]) ghz.cx(q3[0],q3[1]) ghz.cx(q3[1],q3[2])
becomes:
ghz.h(q3[2])
ghz.cx(q3[2],q3[1])
ghz.cx(q3[1],q3[0])
For those who prefer to use the composer, a series of four experiments is also proposed (Figure 1). The results can then be retrieved as *.csv files to perform the calculations.
 |
| Figure 1 |
The set of observables remains the same as that used in the original program of the QISKit Tutorial:
{'00000': 1, '00001': -1, '00010': -1, '00011': 1, '00100': -1, '00101': 1, '00110': 1, '00111': -1}
The results obtained using QISKit are presented in Table 1 and Figure 2.
 |
| Table 1 |
 |
| Figure 2 |
The Mermin polynomial for 3 qubits is obtained by adding the absolute values of the figures present in the last row of Table 1. We obtain 2.99, that is a value slightly higher than the value of 2.65 calculated according to the results reported in the full user guide (here) or the value of 2.85 reported by Alsina and Latorre (there). The current result is well beyond the upper bound for local realism, which is 2, while the theoretical upper bound for quantum theory is 4.
The inspection of Figure 2 reveals the contrast between the distribution observed for the experiment XXX and those observed for the experiments XYY, YXY and YYX. The latter are all alike.
Five-qubit GHZ-state and Mermin inequality.
In this section, the programmation and results using a set of five qubits is briefly reported.
By modifying the four-qubits GHZ tutorial program, it was possible to easily create a QUISKit's program for five qubits, giving the distributions for the ZZZZZ and XXXXX measurements. However, developing the program delivering the 16 distributions necessary to test the corresponding Mermin inequality appeared to be a tedious task, which was all the more disheartening in that it required, in fine, to submit a total of 16 circuits during a single execution phase, with a risk of aborted task. This is why the circuits were realized and executed individually using the composer, which makes it very easy to build each successive circuit from the previous one in a unique collection of experiments. An example of a such a partition, in this case the measurement XYYYY, is shown in Figure 3.
The set of observables, according to the same logic as in the previous case, was chosen as:
The results obtained using the composer are presented in Table 2 and Figure 4.
By modifying the four-qubits GHZ tutorial program, it was possible to easily create a QUISKit's program for five qubits, giving the distributions for the ZZZZZ and XXXXX measurements. However, developing the program delivering the 16 distributions necessary to test the corresponding Mermin inequality appeared to be a tedious task, which was all the more disheartening in that it required, in fine, to submit a total of 16 circuits during a single execution phase, with a risk of aborted task. This is why the circuits were realized and executed individually using the composer, which makes it very easy to build each successive circuit from the previous one in a unique collection of experiments. An example of a such a partition, in this case the measurement XYYYY, is shown in Figure 3.
 |
| Figure 3 |
| 00000 | 00001 | 00010 | 00011 | 00100 | 00101 | 00110 | 00111 |
| -1 | 1 | 1 | -1 | 1 | -1 | -1 | 1 |
| 01000 | 01001 | 01010 | 01011 | 01100 | 01101 | 01110 | 01111 |
| 1 | -1 | -1 | 1 | -1 | 1 | 1 | -1 |
| 10000 | 10001 | 10010 | 10011 | 10100 | 10101 | 10110 | 10111 |
| 1 | -1 | -1 | 1 | -1 | 1 | 1 | -1 |
| 11000 | 11001 | 11010 | 11011 | 11100 | 11101 | 11110 | 11111 |
| -1 | 1 | 1 | -1 | 1 | -1 | -1 | 1 |
The results obtained using the composer are presented in Table 2 and Figure 4.
 |
| Figure 4 |
The Mermin polynomial was computed according to the same rules as for the previous GHZ state from the values listed in the last row of table 2.
The experimental Mermin inequality for 5 qubits was 3.13, lower than the value of 4.05 reported by Alsina and Latorre (there). The current result is well below the upper bound for local realism, which is 8, while the theoretical upper bound for quantum theory is 16 in this case.
The inspection of figure 4 shows that the measurement ZZZZZ confirms that the circuit corresponds to the desired GHZ state ( |00000> +|11111> ) / sqrt(2). Evidently, the XXXXX experiment and the XYYYY experiment produce an histogram with a lower first column (00000 result in classical bits) than the XXXYY experiment. Indeed, this must be expected from quantum theory, since the first two cases correspond to eigenstates whose chosen eigenvalues are the inverse of the third case. Similarly, the inspection of the last row of table 2 shows that the first six values are positive in the range [0.168, 0.268] whereas the ten last values are negative in the range [-0.146, -0,224], corresponding to the theoretical prediction for a perfect computer of a row of six +1 followed by ten -1 in a series of sixteen experiments ordered in such a way.
The Figure 5 highlights the quantum effect of non-locality. Indeed, at first glance a preponderance of the orange color, with columns generally higher, is noted in the top histogram, whereas in the bottom histogram, it is the blue that dominates. These histograms represent the distribution of the average frequencies for each of the possible results 00000 to 11111, at the top for the experiments corresponding to the columns XXXXX to YYYYX of the table 2, at the bottom for the ten experiments corresponding to the columns YYXXX to XXXYY of this table. Blue corresponds to a -1 observable, when orange coresponds to a +1 observable in the 5-qubit Mermin experiment. For a perfect ideal quantum computer, one should expect a top histogram consisting of 16 orange columns of identical height and a bottom histogram composed of the other 16 columns, always of identical height, but blue.
The experimental Mermin inequality for 5 qubits was 3.13, lower than the value of 4.05 reported by Alsina and Latorre (there). The current result is well below the upper bound for local realism, which is 8, while the theoretical upper bound for quantum theory is 16 in this case.
The inspection of figure 4 shows that the measurement ZZZZZ confirms that the circuit corresponds to the desired GHZ state ( |00000> +|11111> ) / sqrt(2). Evidently, the XXXXX experiment and the XYYYY experiment produce an histogram with a lower first column (00000 result in classical bits) than the XXXYY experiment. Indeed, this must be expected from quantum theory, since the first two cases correspond to eigenstates whose chosen eigenvalues are the inverse of the third case. Similarly, the inspection of the last row of table 2 shows that the first six values are positive in the range [0.168, 0.268] whereas the ten last values are negative in the range [-0.146, -0,224], corresponding to the theoretical prediction for a perfect computer of a row of six +1 followed by ten -1 in a series of sixteen experiments ordered in such a way.
The Figure 5 highlights the quantum effect of non-locality. Indeed, at first glance a preponderance of the orange color, with columns generally higher, is noted in the top histogram, whereas in the bottom histogram, it is the blue that dominates. These histograms represent the distribution of the average frequencies for each of the possible results 00000 to 11111, at the top for the experiments corresponding to the columns XXXXX to YYYYX of the table 2, at the bottom for the ten experiments corresponding to the columns YYXXX to XXXYY of this table. Blue corresponds to a -1 observable, when orange coresponds to a +1 observable in the 5-qubit Mermin experiment. For a perfect ideal quantum computer, one should expect a top histogram consisting of 16 orange columns of identical height and a bottom histogram composed of the other 16 columns, always of identical height, but blue.
 |
| Figure 5 |
Discussion
One could discuss the choice of observables in the two cases studied here. The inverse set could have been chosen. David Mermin already made the following remark*: "The specific form of the state vector is unimportant". As the author highlights some paragraphs later in this paper, the important point is to satisfy an inequality, which is in the case of three qubits a, b and c:
The slightly higher value observed for the three-qubit Mermin polynomial might reflect the presence of a simplified circuit with less gates than in the previous studies, but the improvement of the experimental apparatus with a reduction of the error rates can also be invoked.
The lower value than in the study of Alsina and Lattore observed for the five-qubit Mermin polynomial is somewhat unexpected. This could indicate a certain degradation of the experimental device, but in this case the cause is hardly obvious. More likely, the estimate made by these authors from only 3 experiments out of the 16 of the complete set may have been affected by a higher imprecision and have given a result closer to theoretical upper bounds by mere chance.
Finally, these experiments are not loophole free and serve as pedagogical demonstration rather than as experimental evidence.
Finally, these experiments are not loophole free and serve as pedagogical demonstration rather than as experimental evidence.
Conclusion
A simple and straightforward demonstration of the Mermin inequalities for three and five qubit GHZ states is presented here.
The results are broadly comparable to those of other experiments on an older five-qubit quantum computer version made available by the IBM quantum experience. It is important to note that these previous experiments focused on GHZ states different from the one studied here and that the computer architecture required more complicated circuits.
The study of the 3-qubit GHZ state represents a good demonstration of the quantum model and highlights a clear violation of the classical model.
The study of the 5-qubit GHZ state does not demonstrate this violation in a numerical way. This is obviously attributable to the sources of error still present in the experimental device. However, the contemplation of the results of the 16 experiments shows an estimate of the five-qubit operators quite consistent with the theoretical model.
* N. David Mermin. Quantum mysteries revisited. Am. J. Phys., Vol. 58, No. 8 p.731-734, August 1990.


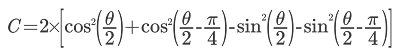
sir i have a doubt about the parities of '01011' and '10111'.
ReplyDeleteI am not sure, but i think parity of '01011' should be +1 and '10111' should be -1.
Please correct me if my understanding is wrong.
Thank you for your remark. You are absolutely right. I made the correction on my excel file and in the blog. The experimental Mermin inequality for 5 qubits is now 3.13, thus a little higher. I corrected also figure 5, with in addition a better design of the column graphic enhancing the point.
DeleteThe reason of my error was typos when I switched in my excel spreadsheet from one possible parity convention to the symmetric one. Not as consequential as the error of Reinhart and Rogoff (https://www.newscientist.com/article/dn23448-how-to-stop-excel-errors-driving-austerity-economics/) but same kind of mistake. Congratulations, you are the Herndon of my modest blog
Thanks for clearing my doubt sir.
Delete