CHSH experiment on a quantum computer
The
experiment proposed in 1969 by John Clauser, Michael Horne, Abner Shimony, and
Richard Holt can now be realized on the quantum computers made available to the
public by IBM.
However different versions of this famous CHSH
experiment are proposed. A new version is described in a recent QISKit tutorial.Here is presented an experimental frame, based on the theoretical frame of this recent tutorial, which can be performed on the newly available ibmqx4 quantum computer either by using a minimally modified version of the Python program or simply the graphical composer. This latter option is indeed readily available for those who don't want investing time in installing Python on their laptop or simply want to use a tablet or even a smartphone.
Theory
The theoretical basis is clearly explained in the QISKit tutorial in the section "CHSH inequality". This section gives the equation describing the input state | Psi(theta) > swept vs. theta.
An interesting feature of this central equation is that the value of C can be derived from it:
This equation appears so simple that a verification was necessary by comparing the results with those of the calculation program of C by the simulator provided in the tutorial. As shown in FIG. 1, the results are almost identical.
 |
| FIG .1 |
Experimental results using QISkit
The part of the program allowing to calculate C on the ibmqx4 was sligtly modified in order to be in accordance with the ibmqx4 settings (see details about the backend here).
In particular, the quantum circuit must now apply a Hadamard gate on q[1], followed by a CNOT from q[1] to q[0]. Here are the required modifications:
In [2]:
backend = 'ibmqx2' # the backend to run on
becomes:
backend = 'ibmqx4' # the backend to run on
bell.h(q[0])
becomes :
bell.h(q[1])
bell.cx(q[0],q[1])
becomes
bell.cx(q[1],q[0])
In [12]:
backend = 'ibmqx2'
becomes:
backend = 'ibmqx4'
The program was run for theta values from 0 to 15 pi/8 by steps of pi/8, using N=8192 shots for each experiment.
The comparison between the theoretical curve (calculated from the above formula) and the experimental data is shown in FIG.2. Maximal violations (theoretically: |2.831|) were seen for theta = pi/4 (C=2.493) and for theta = 5pi/4 (C=-2.405).
 |
| FIG.2 |
Experimental results using the composer
To demonstrate that the same job can be performed using the composer instead of QISKit, four experiments were executed on the ibmqx4, each consisting of N=1024 runs (FIG.3).
Like in the modified QISKit program, a first Hadamard gate is applied to q[1] and a CNOT controlled by q[1] is targeting q[0]. The chosen value for theta is 0.589 (3pi/16), which is introduced as minus theta in a U3 gate applied to q[1] with phi and lambda maintained to zero. This results in applying to q[1] a rotation of minus theta about the y axis on the Bloch sphere .
 |
| FIG.3 |
The results of this set of four experiments are presented in the Table. The observed value for C on the real quantum computer is 2.311 for a theoretical value of 2.774.
 |
| Table |
Conclusion
Either using the QISkit program or the composer on the ibmqx4 quantum computer, a clear violation of the CHSH inequality was observed in the range of theta values where it could be expected.
Remember however that these experiments are not loophole free. For instance, the distance beween the qubits is pretty small, as it can be seen on the first figure of the description given here.
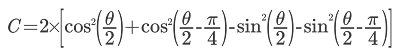

Comments
Post a Comment